Research

As a computational mathematician, my research focuses on the development and rigorous analysis of numerical algorithms. I specialize in designing efficient and robust methods for approximating solutions to partial differential equations (PDEs) or systems of PDEs. I am generally interested in the following research fields:

• Multigrid methods
• PDE-constrained optimization, optimal control problems
• (Stabilized) finite element methods, discontinuous Galerkin methods
• Convection-dominated problems
• Fluid-structure interaction
• Scientific machine learning

Research Projects:

• Efficient numerical methods for optimal control problems.

  • We have designed and analyzed new finite element methods (continuous Galerkin and Discontinuous Galerkin) and multigrid methods for elliptic optimal control problems (with pointwise state constraints). We are now particularly interested in designing finite element methods and multigrid methods for elliptic optimal control problems constrained by convection-diffusion-reaction equations (with pointwise state constraints), especially in the convection-dominated regime.

  • We have investigated the following numerical methods and their corresponding fast solvers:

    • Discontinuous Galerkin methods
    • Hybridizable discontinuous Galerkin methods
    • Edge-averaged finite element methods

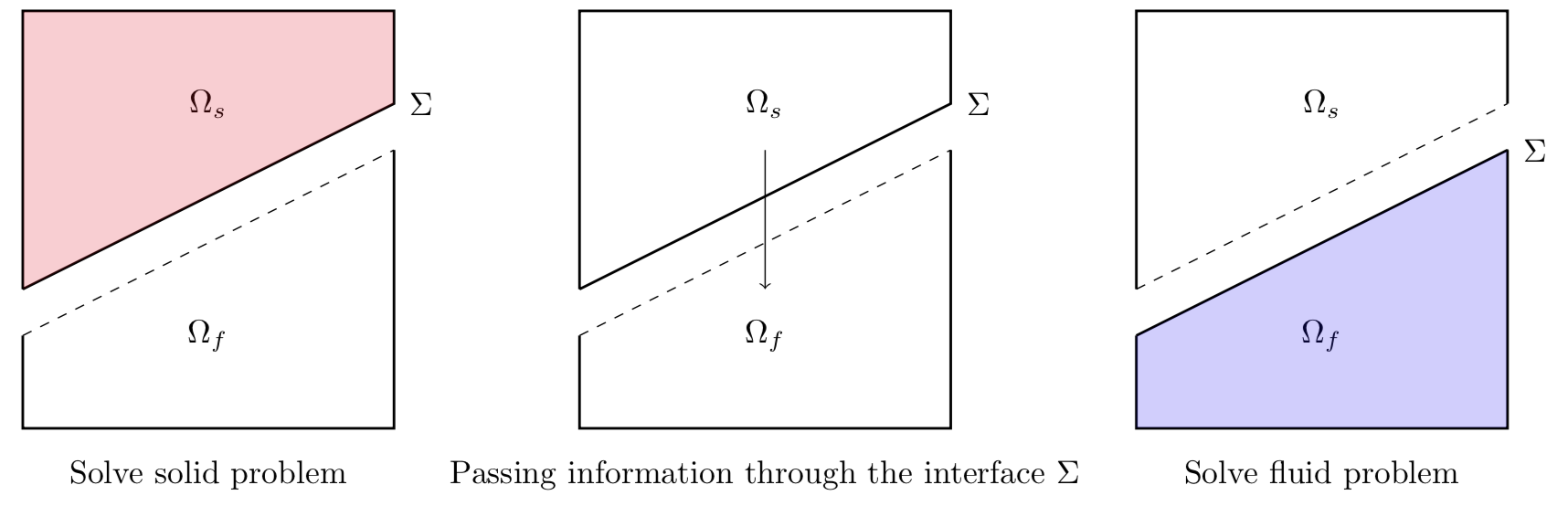
• Fluid-Structure interaction problems.
  • We are also interested in fluid-structure interaction problems. These are multiphysics problem that consists of a fluid problem and a solid problem that interact with each other through an interface. We are particularly interested in Robin-Robin loosely coupled methods, as well as in designing new loosely coupled methods that exhibit higher convergence rates.

  

• Dual-wind discontinuous Galerkin methods for convection-dominated problems.
  • Dual-wind discontinuous Galerkin (DWDG) methods are new discontinuous Galerkin (DG) methods that are derived from a DG differential calculus framework. This framework recovers existing DG methods and also advises construction of new DG methods.

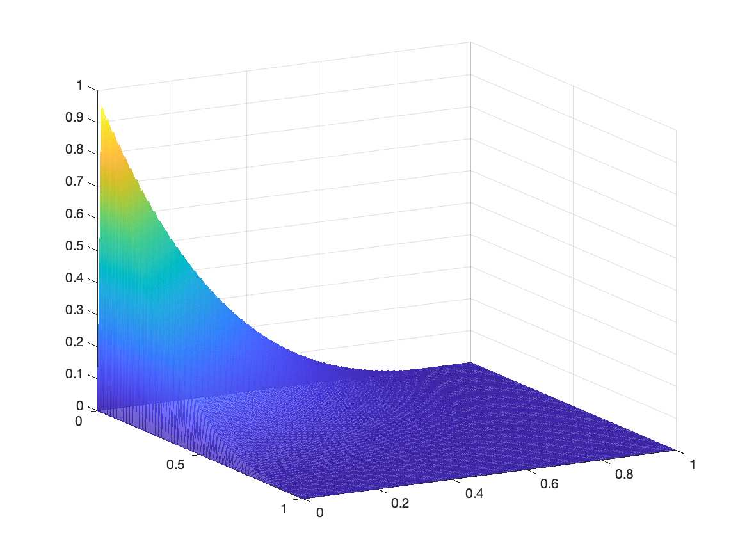
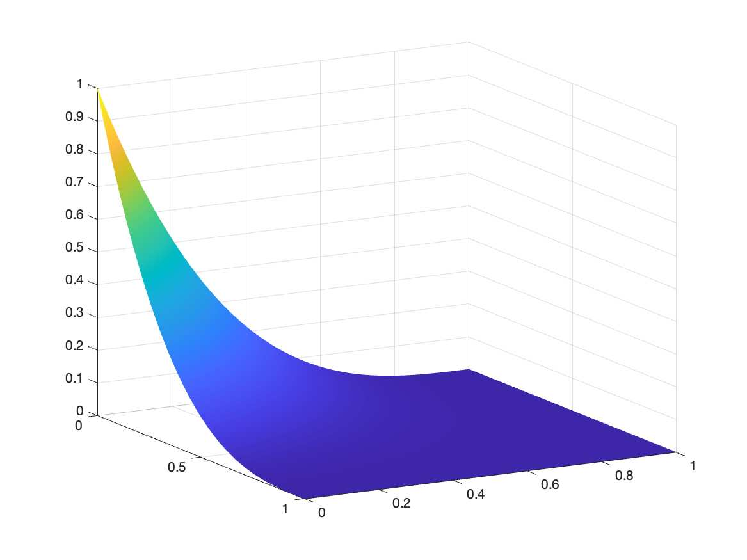
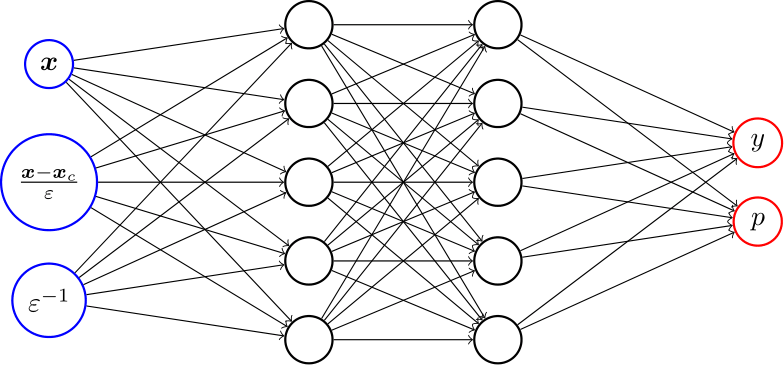
• Physics-informed neural networks (PINNs) for optimal control problems with convection-dominated state equations.
  • PINNs incorporate PDEs into the loss function of neural networks to solve PDEs. We are interested in using PINNs to solve a saddle-point formulation of an optimal control problem with convection-dominated state equations. To tackle this challenging problem, we exploit a recently developed two-scale neural network.